Figurat e ngurta gjeometrike janë trupa të ngurtë që zënë një vëllim jo zero në hapësirën Euklidiane (tre-dimensionale). Këto figura studiohen nga një degë e matematikës e quajtur "gjeometria hapësinore". Njohuritë për vetitë e figurave tredimensionale përdoren në inxhinieri dhe shkenca natyrore. Në artikull do të shqyrtojmë çështjen e figurave gjeometrike tre-dimensionale dhe emrat e tyre.

Trupat gjeometrike

Meqenëse këto trupa kanë një dimension të fundëm në tre drejtime hapësinore, një sistem prej tre boshtesh koordinative përdoret për t'i përshkruar ato në gjeometri. Këto akse kanë vetitë e mëposhtme:

1. Ato janë ortogonale me njëra-tjetrën, domethënë pingul.
2. Këto akse janë të normalizuara, që do të thotë se vektorët bazë të secilit bosht janë me të njëjtën gjatësi.
3. Secili prej boshteve të koordinatave është rezultat i prodhimit vektorial të dy të tjerëve.

Duke folur për figurat vëllimore gjeometrike dhe emrat e tyre, duhet të theksohet se të gjithë i përkasin njërës prej 2 klasave të mëdha:

1. Klasa e poliedrave. Këto figura, bazuar në emrin e klasës, kanë skaje të drejta dhe faqe të sheshta. Një fytyrë është një plan që kufizon një formë. Pika ku bashkohen dy faqe quhet skaj, dhe pika ku bashkohen tre faqe quhet kulm. Polyedrat përfshijnë figurën gjeometrike të një kubi, tetraedronet, prizmat dhe piramidat. Për këto figura është e vlefshme teorema e Euler-it, e cila vendos një lidhje midis numrit të brinjëve (C), skajeve (P) dhe kulmeve (B) për çdo shumëfaqësh. Matematikisht, kjo teoremë shkruhet si më poshtë: C + B = P + 2.
2. Klasa e trupave të rrumbullakët ose trupave të revolucionit. Këto figura kanë të paktën një sipërfaqe që i formon ato që është e lakuar. Për shembull, një top, një kon, një cilindër, një torus.

Sa i përket vetive të figurave vëllimore, duhet të theksohen dy më të rëndësishmet prej tyre:

1. Prania e një vëllimi të caktuar që një figurë zë në hapësirë.
2. Prania e një sipërfaqeje për secilën figurë vëllimore.

Të dyja vetitë për secilën figurë përshkruhen me formula specifike matematikore.

Le të shqyrtojmë më poshtë figurat vëllimore gjeometrike më të thjeshta dhe emrat e tyre: kubi, piramida, prizmi, tetraedri dhe topi.

Figura e kubit: përshkrim

Kubi i figurës gjeometrike është një trup tredimensional i formuar nga 6 rrafshe ose sipërfaqe katrore. Kjo figurë quhet edhe një gjashtëkëndësh i rregullt, pasi ka 6 brinjë, ose një paralelipiped drejtkëndor, pasi përbëhet nga 3 palë brinjë paralele që janë reciprokisht pingul me njëra-tjetrën. Quhet kub, baza e të cilit është katror dhe lartësia është e barabartë me faqen e bazës.

Meqenëse një kub është një shumëfaqësh ose shumëfaqësh, teorema e Euler-it mund të zbatohet për të për të përcaktuar numrin e skajeve të tij. Duke ditur se numri i anëve është 6, dhe kubi ka 8 kulme, numri i skajeve është: P = C + B - 2 = 6 + 8 - 2 = 12.

Nëse shënojmë gjatësinë e anës së një kubi me shkronjën "a", atëherë formulat për vëllimin dhe sipërfaqen e tij do të duken si: V = a 3 dhe S = 6*a 2, përkatësisht.

Figura piramidale

Një piramidë është një shumëfaqësh që përbëhet nga një shumëfaqësh i thjeshtë (baza e piramidës) dhe trekëndësha që lidhen me bazën dhe kanë një kulm të përbashkët (maja e piramidës). Trekëndëshat quhen faqet anësore të piramidës.

Karakteristikat gjeometrike të një piramide varen nga shumëkëndëshi në bazën e saj, si dhe nga fakti nëse piramida është e drejtë apo e zhdrejtë. Një piramidë e drejtë kuptohet si një piramidë për të cilën një vijë e drejtë pingul me bazën, e tërhequr përmes majës së piramidës, e kryqëzon bazën në qendrën e saj gjeometrike.

Një nga piramidat e thjeshta është një piramidë e drejtë katërkëndëshe, në bazën e së cilës shtrihet një katror me anën "a", lartësia e kësaj piramide është "h". Për këtë figurë piramidale, vëllimi dhe sipërfaqja do të jenë të barabarta: V = a 2 *h/3 dhe S = 2*a*√(h 2 +a 2 /4) + a 2, përkatësisht. Duke zbatuar teoremën e Euler-it për të, duke marrë parasysh se numri i faqeve është 5 dhe numri i kulmeve është 5, marrim numrin e skajeve: P = 5 + 5 - 2 = 8.

Figura e katërkëndëshit: përshkrim

Tetraedri i figurës gjeometrike kuptohet si një trup tredimensional i formuar nga 4 faqe. Bazuar në vetitë e hapësirës, ​​fytyra të tilla mund të përfaqësojnë vetëm trekëndësha. Kështu, një tetrahedron është një rast i veçantë i një piramide, e cila ka një trekëndësh në bazën e saj.

Nëse të 4 trekëndëshat që formojnë faqet e një katërkëndëshi janë barabrinjës dhe të barabartë me njëri-tjetrin, atëherë një katërkëndësh i tillë quhet i rregullt. Ky katërkëndor ka 4 faqe dhe 4 kulme, numri i skajeve është 4 + 4 - 2 = 6. Duke zbatuar formulat standarde nga gjeometria e rrafshët për figurën në fjalë, fitojmë: V = a 3 * √2/12 dhe S = √ 3*a 2, ku a është gjatësia e brinjës së një trekëndëshi barabrinjës.

Është interesante të theksohet se në natyrë disa molekula kanë formën e një tetraedri të rregullt. Për shembull, një molekulë metani CH 4, në të cilën atomet e hidrogjenit ndodhen në kulmet e tetraedrit dhe janë të lidhur me atomin e karbonit me lidhje kimike kovalente. Atomi i karbonit ndodhet në qendrën gjeometrike të tetraedrit.

Forma e katërkëndëshit, e cila është e lehtë për t'u prodhuar, përdoret gjithashtu në inxhinieri. Për shembull, forma tetrahedrale përdoret në prodhimin e spirancave për anijet. Vini re se sonda hapësinore e NASA-s Mars Pathfinder, e cila u ul në sipërfaqen e Marsit më 4 korrik 1997, kishte gjithashtu formën e një katërkëndëshi.

Figura e prizmit

Kjo figurë gjeometrike mund të merret duke marrë dy poliedra, duke i vendosur ato paralelisht me njëra-tjetrën në plane të ndryshme të hapësirës dhe duke i lidhur kulmet e tyre në përputhje me rrethanat. Rezultati do të jetë një prizëm, dy poliedra quhen bazat e tij dhe sipërfaqet që lidhin këto poliedra do të kenë formën e paralelogrameve. Një prizëm quhet i drejtë nëse anët e tij (paralelogramet) janë drejtkëndësha.

Një prizëm është një shumëfaqësh, prandaj është e vërtetë për të, për shembull, nëse baza e prizmit është një gjashtëkëndësh, atëherë numri i brinjëve të prizmit është 8, dhe numri i kulmeve është 12. Numri i skajeve do të jetë. të jetë e barabartë me: P = 8 + 12 - 2 = 18. Për një vijë të drejtë një prizëm me lartësi h, në bazën e së cilës shtrihet një gjashtëkëndësh i rregullt me ​​anë a, vëllimi është i barabartë me: V = a 2 *h* √3/4, sipërfaqja është e barabartë me: S = 3*a*(a*√3 + 2*h).

Duke folur për figura të thjeshta gjeometrike vëllimore dhe emrat e tyre, duhet të përmendim topin. Një trup vëllimor i quajtur top kuptohet si një trup që është i kufizuar në një sferë. Nga ana tjetër, një sferë është një koleksion pikash në hapësirë ​​të barabarta nga një pikë, e cila quhet qendra e sferës.

Meqenëse topi i përket klasës së trupave të rrumbullakët, nuk ka koncept të anëve, skajeve dhe kulmeve për të. sfera që kufizon topin gjendet me formulën: S = 4*pi*r 2, dhe vëllimi i topit mund të llogaritet me formulën: V = 4*pi*r 3 /3, ku pi është numri pi. (3.14), r - rrezja e sferës (topit).

Shifrat gjeometrike janë grupe pikash të mbyllura në një rrafsh ose në hapësirë ​​që kufizohen nga një numër i kufizuar vijash. Ato mund të jenë lineare (1D), planare (2D) ose hapësinore (3D).

Çdo trup që ka një formë është një koleksion i formave gjeometrike.

Çdo figurë mund të përshkruhet me një formulë matematikore me shkallë të ndryshme kompleksiteti. Duke filluar nga një shprehje e thjeshtë matematikore deri te shuma e një sërë shprehjesh matematikore.

Parametrat kryesorë matematikorë të figurave gjeometrike janë rrezet, gjatësitë e brinjëve ose skajeve dhe këndet ndërmjet tyre.

Më poshtë janë figurat bazë gjeometrike që përdoren më shpesh në llogaritjet e aplikuara, formulat dhe lidhjet me programet e llogaritjes.

Forma gjeometrike lineare

1. Pika

Një pikë është objekti bazë i matjes. Karakteristika kryesore dhe e vetme matematikore e një pike është koordinata e saj.

2. Linja

Një vijë është një objekt hapësinor i hollë që ka një gjatësi të kufizuar dhe që përfaqëson një zinxhir pikash të lidhura me njëra-tjetrën. Karakteristika kryesore matematikore e një linje është gjatësia e saj.

Një rreze është një objekt i hollë hapësinor me gjatësi të pafundme dhe që përfaqëson një zinxhir pikash të lidhura me njëra-tjetrën. Karakteristikat kryesore matematikore të rrezes janë koordinata e origjinës dhe drejtimit të saj.

Forma të sheshta gjeometrike

1. Rretho

Një rreth është një vend gjeometrik pikash në një plan, distanca nga e cila në qendrën e tij nuk e kalon një numër të caktuar, të quajtur rrezja e këtij rrethi. Karakteristika kryesore matematikore e një rrethi është rrezja e tij.

2. Sheshi

Një katror është një katërkëndësh në të cilin të gjitha këndet dhe të gjitha brinjët janë të barabarta. Karakteristika kryesore matematikore e një katrori është gjatësia e brinjës së tij.

3. Drejtkëndësh

Një drejtkëndësh është një katërkëndësh, këndet e të cilit janë të gjithë 90 gradë (djathtas). Karakteristikat kryesore matematikore të një drejtkëndëshi janë gjatësia e brinjëve të tij.

4. Trekëndësh

Një trekëndësh është një figurë gjeometrike e formuar nga tre segmente që lidhin tre pika (kulmet e trekëndëshit) që nuk shtrihen në të njëjtën drejtëz. Karakteristikat kryesore matematikore të një trekëndëshi janë gjatësia e brinjëve dhe lartësia.

5. Trapez

Një trapez është një katërkëndësh në të cilin dy anët janë paralele dhe dy anët e tjera nuk janë paralele. Karakteristikat kryesore matematikore të një trapezi janë gjatësia e anëve dhe lartësia.

6. Paralelogrami

Një paralelogram është një katërkëndësh, anët e kundërta të të cilit janë paralele. Karakteristikat kryesore matematikore të një paralelogrami janë gjatësia e brinjëve dhe lartësia e tij.

Rombi është një katërkëndësh që i ka të gjitha anët, por këndet e kulmeve të tij nuk janë të barabarta me 90 gradë. Karakteristikat kryesore matematikore të një rombi janë gjatësia e anës dhe lartësia e tij.

8. Elipsa

Një elipsë është një kurbë e mbyllur në një plan, e cila mund të përfaqësohet si një projeksion ortogonal i një seksioni të perimetrit të një cilindri mbi një plan. Karakteristikat kryesore matematikore të një rrethi janë gjatësia e gjysmëboshteve të tij.

Forma gjeometrike vëllimore

1. Topi

Një top është një trup gjeometrik, i cili është një koleksion i të gjitha pikave në hapësirë ​​të vendosura në një distancë të caktuar nga qendra e tij. Karakteristika kryesore matematikore e një topi është rrezja e tij.

Një sferë është guaska e një trupi gjeometrik, i cili është një koleksion i të gjitha pikave në hapësirë ​​të vendosura në një distancë të caktuar nga qendra e tij. Karakteristika kryesore matematikore e një sfere është rrezja e saj.

Një kub është një trup gjeometrik që është një shumëfaqësh i rregullt, secila faqe e të cilit është një katror. Karakteristika kryesore matematikore e një kubi është gjatësia e skajit të tij.

4. Paralelepiped

Një paralelipiped është një trup gjeometrik, i cili është një shumëfaqësh me gjashtë faqe dhe secila prej tyre është një drejtkëndësh. Karakteristikat kryesore matematikore të një paralelipipedi janë gjatësitë e skajeve të tij.

5. Prizma

Një prizëm është një shumëkëndësh, dy nga fytyrat e të cilit janë shumëkëndësha të barabartë të shtrirë në plane paralele, dhe faqet e mbetura janë paralelogramë që kanë anët e përbashkëta me këta shumëkëndësha. Karakteristikat kryesore matematikore të një prizmi janë sipërfaqja e bazës dhe lartësia.

Një kon është një figurë gjeometrike e marrë duke kombinuar të gjitha rrezet që dalin nga një kulm i konit dhe kalojnë nëpër një sipërfaqe të sheshtë. Karakteristikat kryesore matematikore të një koni janë rrezja e bazës dhe lartësia.

7. Piramida

Një piramidë është një shumëfaqësh, baza e të cilit është një shumëkëndësh arbitrar, dhe faqet anësore janë trekëndësha që kanë një kulm të përbashkët. Karakteristikat kryesore matematikore të një piramide janë sipërfaqja e bazës dhe lartësia.

8. Cilindri

Cilindri është një figurë gjeometrike e kufizuar nga një sipërfaqe cilindrike dhe dy plane paralele që e kryqëzojnë atë. Karakteristikat kryesore matematikore të një cilindri janë rrezja dhe lartësia e bazës.

Ju mund t'i kryeni shpejt këto operacione të thjeshta matematikore duke përdorur programet tona online. Për ta bërë këtë, futni vlerën fillestare në fushën përkatëse dhe klikoni butonin.

Kjo faqe paraqet të gjitha figurat gjeometrike që gjenden më shpesh në gjeometri për të përfaqësuar një objekt ose një pjesë të tij në një plan ose në hapësirë.

Ka një numër të pafund formash. Forma është skica e jashtme e një objekti.

Studimi i formave mund të fillojë që në fëmijërinë e hershme, duke tërhequr vëmendjen e fëmijës suaj në botën përreth nesh, e cila përbëhet nga forma (një pjatë është e rrumbullakët, një televizor është drejtkëndor).

Nga mosha dy vjeç, një fëmijë duhet të dijë tre forma të thjeshta - një rreth, një katror, ​​një trekëndësh. Në fillim ai duhet t'i tregojë vetëm kur ju kërkoni. Dhe në moshën tre vjeç, ju tashmë mund t'i emërtoni ato vetë dhe të dalloni një rreth nga një ovale, një katror nga një drejtkëndësh.

Sa më shumë ushtrime të bëjë një fëmijë për të konsoliduar forma, aq më shumë forma të reja do të kujtojë.

Nxënësi i ardhshëm i klasës së parë duhet të njohë të gjitha format e thjeshta gjeometrike dhe të jetë në gjendje të bëjë aplikime prej tyre.

Çfarë quajmë një figurë gjeometrike?

Një figurë gjeometrike është një standard me të cilin mund të përcaktoni formën e një objekti ose pjesëve të tij.

Figurat ndahen në dy grupe: figura të sheshta, figura tredimensionale.

Figurat e rrafshit i quajmë ato figura që ndodhen në të njëjtin rrafsh. Këto përfshijnë rrethin, ovalin, trekëndëshin, katërkëndëshin (drejtkëndësh, katror, ​​trapez, romb, paralelogram) dhe të gjitha llojet e shumëkëndëshave.

Figurat tredimensionale përfshijnë: sferën, kubin, cilindrin, konin, piramidën. Këto janë ato forma që kanë lartësi, gjerësi dhe thellësi.

Ndiqni dy këshilla të thjeshta kur shpjegoni forma gjeometrike:

1. Durim. Ajo që na duket e thjeshtë dhe logjike neve, të rriturve, do të duket thjesht e pakuptueshme për një fëmijë.
2. Provoni të vizatoni forma me fëmijën tuaj.
3. Nje loje. Filloni të mësoni forma në një mënyrë lozonjare. Ushtrime të mira për konsolidimin dhe studimin e formave të sheshta janë aplikime nga format gjeometrike. Për ato voluminoze, mund të përdorni lojëra të gatshme të blera në dyqan, si dhe të zgjidhni aplikacione ku mund të prisni dhe ngjitni një formë voluminoze.

Shifrat më të thjeshta gjeometrike përfshijnë një pikë, një vijë të drejtë, një segment, një rreze, një gjysmë plan dhe një kënd.

Edhe ndër figurat më të thjeshta, spikat më e thjeshta - kjo pika. Të gjitha figurat e tjera përbëhen nga shumë pika. Në gjeometri, është zakon që pikat të shënohen me shkronja latine të mëdha (kapitale). Për shembull, pika A, pika L.

Drejt- kjo është një vijë e pafundme në të cilën nëse merrni dy pika, atëherë distanca më e shkurtër midis tyre do të kalojë përgjatë kësaj vije të drejtë. Linjat e drejtpërdrejta më së shpeshti shënohen me një shkronjë latine të vogël (të vogël). Për shembull, drejtëza a, drejtëza b. Megjithatë, në disa raste ka dy të mëdha. Për shembull, drejt AB, drejt CD.

Segmenti i linjës- kjo është një pjesë e një vije të drejtë së bashku me pikat që kufizojnë këtë pjesë. Kjo do të thotë, një segment përbëhet nga dy pika që shtrihen në një vijë dhe një seksion i kësaj linje midis këtyre dy pikave. Pikat e segmentit quhen skajet e segmentit. Është e qartë se dy pika nuk duhet të përkojnë, domethënë të shtrihen në të njëjtin vend në një vijë të drejtë. Përndryshe, segmenti do të ketë gjatësi zero dhe në thelb do të jetë një pikë. Segmentet përcaktohen me dy shkronja të mëdha, të cilat tregojnë skajet e segmentit. Për shembull, nëse skajet e një segmenti janë pikat A dhe B, atëherë segmenti do të caktohet si AB.

Nëse një vijë e drejtë ndahet në dy pjesë me një pikë, atëherë dy rreze. Njëra vjen nga një pikë në një drejtim, dhe tjetra në tjetrën. Kështu, nëse një segment është i kufizuar në të dy skajet, atëherë rrezja ka vetëm njërën anë, dhe ana tjetër e rrezes është e pafundme, si një vijë e drejtë. Rrezet përcaktohen në të njëjtën mënyrë si vijat e drejta: ose me një shkronjë të vogël ose me dy të mëdha.

Gjysmë aeroplan- kjo është një pjesë e aeroplanit që shtrihet në njërën anë ose në tjetrën të vijës së drejtë. Nga kjo rrjedh se vija e drejtë e ndan rrafshin në dy gjysmë-rrafshe, dhe vetë është kufiri i tyre.

Këndi, përbëhet nga një pikë dhe dy rreze që shtrihen prej saj. Ky koncept i një këndi është i afërt me atë se si koncepti i një rrezeje u prezantua më lart: një pikë ndan një vijë të drejtë në dy rreze. Por në atë rast ne po flisnim për faktin se të dy rrezet shtrihen në të njëjtën vijë të drejtë. Por këtu kjo nuk është aspak e nevojshme. Dy rreze mund t'i përkasin linjave të ndryshme të drejta, gjëja kryesore është se pika nga e cila burojnë është e zakonshme për ta. Kjo pikë quhet kulmi i këndit, ndërsa rrezet quhen anët e këndit.

Këndet përcaktohen ndryshe - me një shkronjë, dy, tre. Por ato gjithmonë paraprihen nga shenja ∠ (kënd). Për shembull ∠ABC, ∠B, ∠ac.

Teksti i veprës është postuar pa imazhe dhe formula.
Versioni i plotë i veprës gjendet në skedën "Work Files" në format PDF

Prezantimi

Gjeometria është një nga komponentët më të rëndësishëm të edukimit matematikor, i nevojshëm për përvetësimin e njohurive specifike rreth hapësirës dhe aftësive praktikisht domethënëse, formimin e një gjuhe për përshkrimin e objekteve në botën përreth, për zhvillimin e imagjinatës dhe intuitës hapësinore, kulturës matematikore. , si dhe për edukimin estetik. Studimi i gjeometrisë kontribuon në zhvillimin e të menduarit logjik dhe formimin e aftësive të provës.

Kursi i gjeometrisë në klasën e 7-të sistematizon njohuritë për figurat më të thjeshta gjeometrike dhe vetitë e tyre; prezantohet koncepti i barazisë së figurave; zhvillohet aftësia për të vërtetuar barazinë e trekëndëshave duke përdorur shenjat e studiuara; paraqitet një klasë problemesh që përfshijnë ndërtimin duke përdorur një busull dhe vizore; prezantohet një nga konceptet më të rëndësishme - koncepti i vijave paralele; konsiderohen vetitë e reja interesante dhe të rëndësishme të trekëndëshave; konsiderohet një nga teoremat më të rëndësishme në gjeometri - teorema mbi shumën e këndeve të një trekëndëshi, e cila na lejon të klasifikojmë trekëndëshat sipas këndeve (akut, drejtkëndor, i mpirë).

Gjatë orëve të mësimit, veçanërisht kur kaloni nga një pjesë e mësimit në tjetrin, duke ndryshuar aktivitetet, lind pyetja e ruajtjes së interesit për klasat. Kështu, relevante Shtrohet pyetja për përdorimin e detyrave në klasat e gjeometrisë që përfshijnë gjendjen e një situate problemore dhe elemente të krijimtarisë. Kështu, qëllimi Ky studim synon të sistemojë detyrat e përmbajtjes gjeometrike me elemente të krijimtarisë dhe situata problemore.

Objekti i studimit: Detyrat e gjeometrisë me elemente të krijimtarisë, argëtimit dhe situatave problemore.

Objektivat e kërkimit: Analizoni detyrat ekzistuese të gjeometrisë që synojnë zhvillimin e logjikës, imagjinatës dhe të menduarit krijues. Tregoni se si mund të zhvilloni interes për këtë temë duke përdorur teknika argëtuese.

Rëndësia teorike dhe praktike e hulumtimitështë se materiali i mbledhur mund të përdoret në procesin e mësimeve shtesë në gjeometri, përkatësisht në olimpiada dhe gara në gjeometri.

Qëllimi dhe struktura e studimit:

Studimi përbëhet nga një hyrje, dy kapituj, një përfundim, një bibliografi, përmban 14 faqe teksti kryesor të shtypur, 1 tabelë, 10 figura.

Kapitulli 1. FIGURA GJEOMETRIKE E SHFESË. KONCEPTE DHE PËRKUFIZIMET THEMELORE

1.1. Figurat bazë gjeometrike në arkitekturën e ndërtesave dhe strukturave

Në botën përreth nesh ka shumë objekte materiale të formave dhe madhësive të ndryshme: ndërtesa banimi, pjesë makinerish, libra, bizhuteri, lodra etj.

Në gjeometri në vend të fjalës objekt thonë figurë gjeometrike, ndërsa figurat gjeometrike i ndajnë në të sheshta dhe hapësinore. Në këtë punë, ne do të shqyrtojmë një nga seksionet më interesante të gjeometrisë - planimetrinë, në të cilën merren parasysh vetëm figurat e rrafshët. Planimetria(nga latinishtja planum - "aeroplan", greqishtja e lashtë μετρεω - "masë") - një pjesë e gjeometrisë Euklidiane që studion figurat dydimensionale (me një plan), domethënë figura që mund të vendosen brenda të njëjtit plan. Një figurë e sheshtë gjeometrike është ajo në të cilën të gjitha pikat shtrihen në të njëjtin rrafsh. Çdo vizatim i bërë në një fletë letre jep një ide të një figure të tillë.

Por përpara se të shqyrtojmë figurat e sheshta, është e nevojshme të njihemi me figura të thjeshta, por shumë të rëndësishme, pa të cilat figurat e sheshta thjesht nuk mund të ekzistojnë.

Figura më e thjeshtë gjeometrike është pika. Kjo është një nga figurat kryesore të gjeometrisë. Është shumë i vogël, por përdoret gjithmonë për të ndërtuar forma të ndryshme në aeroplan. Pika është figura kryesore për absolutisht të gjitha ndërtimet, madje edhe kompleksitetin më të lartë. Nga pikëpamja matematikore, një pikë është një objekt hapësinor abstrakt që nuk ka karakteristika të tilla si zona ose vëllimi, por në të njëjtën kohë mbetet një koncept themelor në gjeometri.

Drejt- një nga konceptet themelore të gjeometrisë Në një paraqitje sistematike të gjeometrisë, një vijë e drejtë zakonisht merret si një nga konceptet fillestare, e cila përcaktohet vetëm në mënyrë indirekte nga aksiomat e gjeometrisë (Euklidiane). Nëse baza për ndërtimin e gjeometrisë është koncepti i distancës midis dy pikave në hapësirë, atëherë një vijë e drejtë mund të përkufizohet si një vijë përgjatë së cilës rruga është e barabartë me distancën midis dy pikave.

Linjat e drejta në hapësirë ​​mund të zënë pozicione të ndryshme, le të shqyrtojmë disa prej tyre dhe të japim shembuj që gjenden në pamjen arkitekturore të ndërtesave dhe strukturave (Tabela 1):

Tabela 1

Vijat paralele	Vetitë e drejtëzave paralele
	Nëse linjat janë paralele, atëherë parashikimet e tyre me të njëjtin emër janë paralele:	Essentuki, ndërtesa e banjës me baltë (foto nga autori)
Vijat kryqëzuese	Vetitë e drejtëzave të kryqëzuara	Shembuj në arkitekturën e ndërtesave dhe strukturave
	Linjat kryqëzuese kanë një pikë të përbashkët, domethënë, pikat e kryqëzimit të projeksioneve të tyre me të njëjtin emër shtrihen në një vijë të përbashkët lidhjeje:	Ndërtesat "malore" në Tajvan https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
Linjat e kalimit	Vetitë e vijave të anuar	Shembuj në arkitekturën e ndërtesave dhe strukturave
	Vijat e drejta që nuk shtrihen në të njëjtin rrafsh dhe nuk janë paralele me njëra-tjetrën janë të kryqëzuara. Asnjëra nuk është një linjë e përbashkët komunikimi. Nëse drejtëzat e kryqëzuara dhe ato paralele shtrihen në të njëjtin rrafsh, atëherë drejtëzat e kryqëzuara shtrihen në dy rrafshe paralele.	Robert, Hubert - Villa Madama afër Romës https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287

1.2. Forma të sheshta gjeometrike. Vetitë dhe Përkufizimet

Duke vëzhguar format e bimëve dhe kafshëve, malet dhe gjarpërinjtë e lumenjve, tiparet e peizazhit dhe planetët e largët, njeriu huazoi nga natyra format, përmasat dhe vetitë e saj të sakta. Nevojat materiale i shtynë njerëzit të ndërtonin shtëpi, të bënin vegla pune dhe gjuetie, të skalitnin enët nga balta, e kështu me radhë. E gjithë kjo gradualisht kontribuoi në faktin që njeriu arriti të kuptonte konceptet themelore gjeometrike.

Katërkëndëshat:

Paralelogrami(greqishtja e lashtë παραλληλόγραμμον nga παράλληλος - paralel dhe γραμμή - vijë, vijë) është një katërkëndësh, anët e kundërta të të cilit janë paralele në çift, domethënë shtrihen në drejtëza paralele.

Shenjat e një paralelogrami:

Një katërkëndësh është paralelogram nëse plotësohet një nga kushtet e mëposhtme: 1. Nëse në një katërkëndësh brinjët e kundërta janë të barabarta në çift, atëherë katërkëndëshi është paralelogram. 2. Nëse në një katërkëndësh diagonalet priten dhe ndahen përgjysmë nga pika e prerjes, atëherë ky katërkëndësh është paralelogram. 3. Nëse dy brinjë të një katërkëndëshi janë të barabarta dhe paralele, atëherë ky katërkëndësh është paralelogram.

Një paralelogram këndet e të cilit janë të gjitha kënde të drejta quhet drejtkëndësh.

Një paralelogram në të cilin të gjitha brinjët janë të barabarta quhet diamanti

Trapezoid - Ai është një katërkëndësh në të cilin dy brinjët janë paralele dhe dy brinjët e tjera nuk janë paralele. Gjithashtu, një trapez është një katërkëndësh në të cilin një palë brinjë të kundërta është paralele, dhe anët nuk janë të barabarta me njëra-tjetrën.

Trekëndëshiështë figura më e thjeshtë gjeometrike e formuar nga tre segmente që lidhin tre pika që nuk shtrihen në të njëjtën drejtëz. Këto tre pika quhen kulme trekëndëshi, dhe segmentet janë anët trekëndëshi.Është pikërisht për shkak të thjeshtësisë së tij që trekëndëshi ishte baza e shumë matjeve. Gjeodetët e tokës, kur llogaritin sipërfaqet e tokës, dhe astronomët, kur gjejnë distanca nga planetët dhe yjet, përdorin vetitë e trekëndëshave. Kështu lindi shkenca e trigonometrisë - shkenca e matjes së trekëndëshave, e shprehjes së brinjëve përmes këndeve të saj. Sipërfaqja e çdo shumëkëndëshi shprehet përmes sipërfaqes së një trekëndëshi: mjafton ta ndani këtë shumëkëndësh në trekëndësha, të llogarisni sipërfaqet e tyre dhe të shtoni rezultatet. Vërtetë, nuk ishte e mundur menjëherë të gjesh formulën e saktë për sipërfaqen e një trekëndëshi.

Vetitë e trekëndëshit u studiuan veçanërisht në mënyrë aktive në shekujt 15-16. Këtu është një nga teoremat më të bukura të asaj kohe, për shkak të Leonhard Euler:

Një punë e madhe në gjeometrinë e trekëndëshit, e kryer në shekujt XY-XIX, krijoi përshtypjen se gjithçka dihej tashmë për trekëndëshin.

shumëkëndësh -është një figurë gjeometrike, zakonisht e përcaktuar si një polivijë e mbyllur.

Rretho- vendndodhja gjeometrike e pikave në rrafsh, distanca nga e cila në një pikë të caktuar, e quajtur qendër e rrethit, nuk e kalon një numër të caktuar jo negativ, të quajtur rrezja e këtij rrethi. Nëse rrezja është zero, atëherë rrethi degjeneron në një pikë.

Ekzistojnë një numër i madh i formave gjeometrike, të gjitha ato ndryshojnë në parametra dhe veti, ndonjëherë të habitshme me format e tyre.

Për të kujtuar dhe dalluar më mirë figurat e sheshta sipas vetive dhe karakteristikave, dola me një përrallë gjeometrike, të cilën dëshiroj t'jua paraqes në paragrafin tjetër.

Kapitulli 2. GJEGJEGRA NGA FIGURAT GJEOMETRIKE TË SHPESHTA

2.1.Gjëegjëza për ndërtimin e një figure komplekse nga një grup elementesh gjeometrike të sheshta.

Pasi studiova format e sheshta, pyeta veten nëse kishte ndonjë problem interesant me format e sheshta që mund të përdoreshin si lojëra ose enigma. Dhe problemi i parë që gjeta ishte enigma Tangram.

Ky është një enigmë kineze. Në Kinë quhet "chi tao tu", ose një enigmë mendore me shtatë pjesë. Në Evropë, emri "Tangram" ka shumë të ngjarë të lindi nga fjala "tan", që do të thotë "kinez" dhe rrënja "gram" (greqisht - "shkronjë").

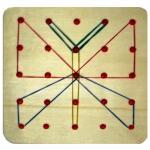
Së pari ju duhet të vizatoni një katror 10 x 10 dhe ta ndani në shtatë pjesë: pesë trekëndësha 1-5 , katror 6 dhe paralelogrami 7 . Thelbi i enigmës është të përdorësh të shtatë pjesët për të bashkuar figurat e paraqitura në figurën 3.

Fig.3. Elemente të lojës "Tangram" dhe forma gjeometrike

Fig.4. Detyrat Tangram

Është veçanërisht interesante të bëhen shumëkëndësha "në formë" nga figura të sheshta, duke ditur vetëm skicat e objekteve (Fig. 4). Unë dola me disa nga këto detyra skicë vetë dhe ua tregova këto detyra shokëve të mi të klasës, të cilët me kënaqësi filluan të zgjidhin detyrat dhe krijuan shumë figura interesante poliedrike, të ngjashme me skicat e objekteve në botën përreth nesh.

Për të zhvilluar imagjinatën, mund të përdorni edhe forma të tilla enigmash argëtuese si detyra për prerjen dhe riprodhimin e figurave të dhëna.

Shembulli 2. Detyrat e prerjes (parketimit) mund të duken, në shikim të parë, mjaft të ndryshme. Megjithatë, shumica e tyre përdorin vetëm disa lloje bazë prerjesh (zakonisht ato që mund të përdoren për të krijuar një tjetër nga një paralelogram).

Le të shohim disa teknika të prerjes. Në këtë rast, ne do të quajmë shifra të prera shumëkëndëshat.

Oriz. 5. Teknikat e prerjes

Figura 5 tregon forma gjeometrike nga të cilat mund të mblidhni kompozime të ndryshme zbukuruese dhe të krijoni një zbukurim me duart tuaja.

Shembulli 3. Një detyrë tjetër interesante që mund ta realizoni vetë dhe ta shkëmbeni me nxënës të tjerë dhe kushdo që mbledh më shumë pjesë të prera shpallet fitues. Mund të ketë mjaft detyra të këtij lloji. Për kodim, mund të merrni të gjitha format gjeometrike ekzistuese, të cilat priten në tre ose katër pjesë.

Fig. 6. Shembuj të detyrave të prerjes:

------ - shesh i rikrijuar; - prerë me gërshërë;

Figura bazë

2.2 Shifra me përmasa të barabarta dhe të përbëra

Le të shqyrtojmë një teknikë tjetër interesante për prerjen e figurave të sheshta, ku "heronjtë" kryesorë të prerjeve do të jenë poligonet. Gjatë llogaritjes së sipërfaqeve të shumëkëndëshave, përdoret një teknikë e thjeshtë e quajtur metoda e ndarjes.

Në përgjithësi, shumëkëndëshat quhen të barabarta nëse, pas prerjes së shumëkëndëshit në një mënyrë të caktuar F në një numër të kufizuar pjesësh, është e mundur, duke i renditur këto pjesë ndryshe, të formohet një shumëkëndësh H prej tyre.

Kjo çon në sa vijon teorema: Shumëkëndëshat me madhësi të njëjtë kanë të njëjtën sipërfaqe, kështu që ata do të konsiderohen të barabartë në sipërfaqe.

Duke përdorur shembullin e poligoneve ekuipartite, mund të konsiderojmë një prerje kaq interesante si shndërrimi i një "kryqi grek" në një katror (Fig. 7).

Fig.7. Transformimi i "Kryqit Grek"

Në rastin e një mozaiku (parketi) të përbërë nga kryqe greke, paralelogrami i periudhave është një katror. Problemin mund ta zgjidhim duke mbivendosur një mozaik të bërë me katrorë mbi një mozaik të formuar me ndihmën e kryqeve, në mënyrë që pikat kongruente të njërit mozaik të përkojnë me pikat kongruente të tjetrit (Fig. 8).

Në figurë, pikat kongruente të mozaikut të kryqeve, përkatësisht qendrat e kryqeve, përkojnë me pikat kongruente të mozaikut "katror" - kulmet e katrorëve. Duke lëvizur paralelisht mozaikun katror, ​​do të marrim gjithmonë një zgjidhje për problemin. Për më tepër, problemi ka disa zgjidhje të mundshme nëse përdoret ngjyra gjatë kompozimit të ornamentit të parketit.

Fig.8. Parket i bërë nga një kryq grek

Një shembull tjetër i figurave me proporcion të barabartë mund të konsiderohet duke përdorur shembullin e një paralelogrami. Për shembull, një paralelogram është i barabartë me një drejtkëndësh (Fig. 9).

Ky shembull ilustron metodën e ndarjes, e cila konsiston në llogaritjen e sipërfaqes së një shumëkëndëshi duke u përpjekur ta ndajmë atë në një numër të kufizuar pjesësh në atë mënyrë që këto pjesë të mund të përdoren për të krijuar një shumëkëndësh më të thjeshtë, sipërfaqen e të cilit ne tashmë e dimë.

Për shembull, një trekëndësh është i barabartë me një paralelogram që ka të njëjtën bazë dhe gjysmën e lartësisë. Nga ky pozicion nxirret lehtësisht formula për sipërfaqen e një trekëndëshi.

Vini re se teorema e mësipërme gjithashtu vlen teorema e kundërt: nëse dy shumëkëndësha janë të barabartë në madhësi, atëherë ato janë ekuivalente.

Kjo teoremë, e vërtetuar në gjysmën e parë të shekullit XIX. nga matematikani hungarez F. Bolyai dhe oficeri gjerman dhe dashnor i matematikës P. Gerwin, mund të përfaqësohen në këtë mënyrë: nëse ka një tortë në formën e një poligoni dhe një kuti poligonale me një formë krejtësisht të ndryshme, por të njëjtën zonë. , më pas mund ta prisni tortën në një numër të kufizuar copash (pa i kthyer me krem ​​poshtë) që mund të vendosen në këtë kuti.

konkluzioni

Si përfundim, dua të theksoj se ka mjaft probleme për figurat e sheshta në burime të ndryshme, por ato që më interesuan ishin ato në bazë të të cilave më duhej të dilja me problemet e mia të enigmës.

Në fund të fundit, duke zgjidhur probleme të tilla, jo vetëm që mund të grumbulloni përvojë jetësore, por edhe të fitoni njohuri dhe aftësi të reja.

Në enigma, kur ndërtoj veprime-lëvizje duke përdorur rrotullime, ndërrime, përkthime në një aeroplan ose kompozime të tyre, kam krijuar në mënyrë të pavarur imazhe të reja, për shembull, figura poliedrike nga loja "Tangram".

Dihet se kriteri kryesor për lëvizshmërinë e të menduarit të një personi është aftësia, nëpërmjet imagjinatës rindërtuese dhe krijuese, për të kryer veprime të caktuara brenda një periudhe të caktuar kohore, dhe në rastin tonë, lëvizje të figurave në një plan. Prandaj, studimi i matematikës dhe në veçanti i gjeometrisë në shkollë do të më japë edhe më shumë njohuri për t'i zbatuar më vonë në aktivitetet e mia profesionale të ardhshme.

Bibliografi

1. Pavlova, L.V. Qasje jo tradicionale për mësimin e vizatimit: një libër shkollor / L.V. Pavlova. - Nizhny Novgorod: Shtëpia Botuese NSTU, 2002. - 73 f.

2. Fjalor Enciklopedik i një Matematikani të Ri / Përmbledhje. A.P. Savin. - M.: Pedagogji, 1985. - 352 f.

3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane

4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053

Shtojca 1

Pyetësor për shokët e klasës

1. A e dini se çfarë është një enigmë Tangram?

2. Çfarë është një "kryq grek"?

3. A do të të interesonte të dinit se çfarë është "Tangram"?

4. A do t'ju interesonte të dini se çfarë është "kryqi grek"?

Janë anketuar 22 nxënës të klasës së 8-të. Rezultatet: 22 studentë nuk e dinë se çfarë është "Tangram" dhe "Kryqi grek". 20 studentë do të ishin të interesuar të mësonin se si të përdorin enigmën Tangram, të përbërë nga shtatë figura të sheshta, për të marrë një figurë më komplekse. Rezultatet e anketës janë përmbledhur në një diagram.

Shtojca 2

Elemente të lojës "Tangram" dhe forma gjeometrike

Transformimi i "Kryqit Grek"